Worksheet on Simplification | Simplify Expressions

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

In worksheet on simplification, the questions are based in order to simplify expressions involving more than one bracket by using the steps of removal of brackets. This exercise sheet on simplifications has different types of questions that can be practiced by the students to get more ideas to simplify the expressions.

BODMAS is an important rule in mathematics that tells us the correct order to solve a mathematical expression. When we see a problem with many operations like addition, subtraction, multiplication, and division, we cannot solve it randomly. If we do, we may get the wrong answer.

So, we use BODMAS to solve problems step by step in the correct order.

BODMAS stands for:

👉 B – Brackets
👉 O – Orders (powers, roots)
👉 D – Division
👉 M – Multiplication
👉 A – Addition
👉 S – Subtraction

This rule helps students understand how to simplify expressions correctly and avoid confusion.

What is Order of Operations?

The order of operations means the sequence in which mathematical operations should be performed. For example, in the expression:

👉 6 + 4 × 3

If we add first, we get the wrong answer.

According to BODMAS, we must multiply first and then add.

So,
4 × 3 = 12
6 + 12 = 18 ✔

This rule is also known worldwide as Order of Operations and in some countries it is called PEMDAS.

Printable Worksheet on Measurement

BODMAS Ladder

$Worksheet on Simplification | Simplify Expressions$

Free Worksheet on Simplification – #Answers

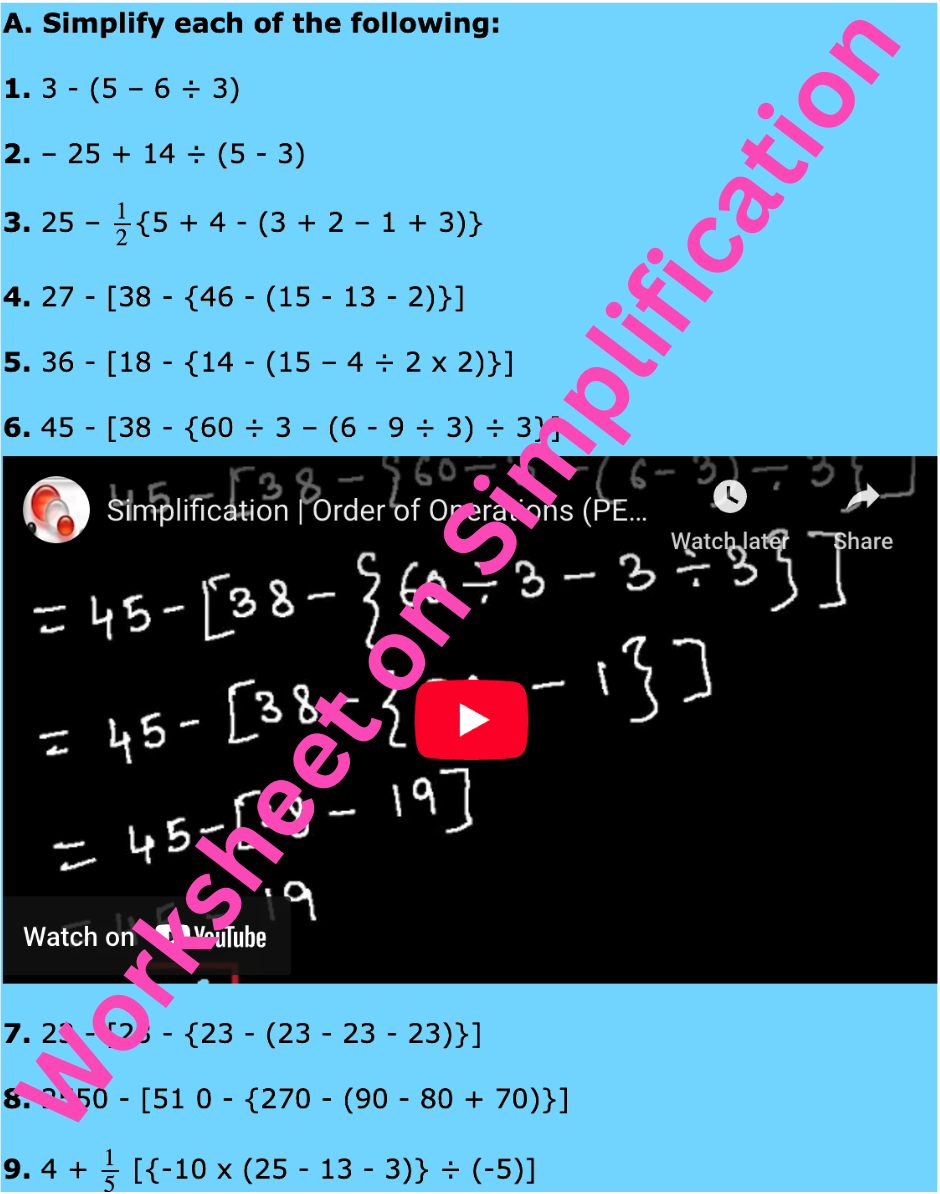
A. Simplify each of the following:

1. 3 – (5 – 6 ÷ 3)

2. – 25 + 14 ÷ (5 – 3)

3. 25 – $\frac{1}{2}${5 + 4 – (3 + 2 – 1 + 3)}

4. 27 – [38 – {46 – (15 – 13 – 2)}]

5. 36 – [18 – {14 – (15 – 4 ÷ 2 x 2)}]

6. 45 – [38 – {60 ÷ 3 – (6 – 9 ÷ 3) ÷ 3}]

7. 23 – [23 – {23 – (23 – 23 – 23)}]

8. 2550 – [51 0 – {270 – (90 – 80 + 70)}]

9. 4 + $\frac{1}{5}$ [{-10 x (25 – 13 – 3)} ÷ (-5)]

10. 22 – $\frac{1}{4}$ {-5 – (- 48) ÷ (-16)}

11. 63 – (-3) {-2 – 8 – 3} ÷ 3{5 + (-2) (-1)}

12. [29 – (-2) {6 – (7 – 3)}] ÷ [3 x {5 + (-3) x (-2)}]

B. Using brackets, write a mathematical expression for each of the following:

1. Nine multiplied by the sum of two and five.

2. Twelve divided by the sum of one and three.

3. Twenty divided by the difference of seven and two.

4. Eight subtracted from the product of two and three.

5. Forty divided by one more than the sum of nine and ten.

6. Two multiplied by one less than the difference of nineteen and six.

C. Simplify the following fractions using BODMAS/PEMDAS Rules:

1. ($\frac{1}{9}$ + $\frac{1}{2}$) × 2$\frac{3}{8}$ + 5$\frac{1}{9}$

2. ($\frac{2}{5}$ + $\frac{3}{8}$) ÷ $\frac{2}{3}$ × 2 – 1$\frac{1}{9}$

3. 14 + [5 {4 + ($\frac{2}{7}$ of 63)}]

4. 49 [6 {5 (25 × $\frac{3}{5}$)}]

5. (8 × 6) ÷ 2 + 30 ÷ (5 × 2) – 3

6. $\frac{5}{6}$ + ($\frac{3}{4}$ × $\frac{5}{9}$) ÷ $\frac{1}{12}$ – $\frac{3}{4}$

7. (14 × 9) ÷ 3 + 12 ÷ (4 × 2) – 2

8. (25 × 6) × 2 – 16 ÷ (9 × 3) – 3

9. $\frac{5}{8}$ × of [8 + {4 (24 + $\overline{9 – 3}$)}] ÷ 4

10. $\frac{3}{5}$ × [$\frac{4}{3}$ + [6 (17 – $\overline{9 – 4}$)]

11. 9 + [7 {2 + ($\frac{3}{4}$ of 48)}] ÷ $\frac{2}{3}$

12. 4 [54 ÷ {4 + (12 – 10)}]

13. 50 ÷ [4 + {8 – (16 × $\frac{1}{4}$)}] + 8

14. 45 + [$\frac{1}{15}$ × {4 (25 ÷ $\frac{1}{5}$)}]

15. 4$\frac{4}{5}$ + ($\frac{4}{5}$ – $\overline{\frac{1}{4} – \frac{1}{5}}$) of 20

16. $\frac{2}{15}$ + {3 ($\frac{3}{4}$ of 8)} ÷ 3

17. 7$\frac{8}{9}$ – ($\frac{4}{9}$ – $\overline{\frac{1}{6} – \frac{1}{9}}$) of 2$\frac{1}{4}$

18. $\frac{3}{15}$ + ($\frac{7}{30}$ ÷ $\frac{1}{15}$) + 3(6 + 3)

19. $\frac{3}{16}$ + ($\frac{5}{8}$ ÷ $\frac{1}{4}$) + 3(6 – 4)

20. $\frac{2}{3}$ × of ($\frac{4}{9}$ – $\frac{1}{18}$) ÷ 3 $\frac{4}{27}$

21. $\frac{3}{4}$ × ($\frac{4}{9}$ – $\frac{1}{4}$) ÷ $\frac{5}{36}$

22. 4$\frac{1}{3}$ × 4$\frac{1}{2}$ ÷ (4$\frac{1}{2}$ + 2$\frac{1}{4}$)

23. $\frac{1}{3}$ of 2$\frac{13}{33}$ × 3$\frac{1}{4}$ ÷ ($\frac{1}{9}$ – $\frac{1}{18}$) + $\frac{2}{9}$

24. $\frac{2}{9}$ of 2$\frac{1}{3}$ × 3$\frac{1}{3}$ ÷ ($\frac{1}{9}$ + $\frac{2}{3}$)

25. 2$\frac{1}{3}$ + {4$\frac{3}{4}$ × (1$\frac{1}{3}$ – $\frac{2}{3}$)]

26. 24 + [9 – {2 + (2 × $\frac{3}{8}$)}]

27. 4$\frac{1}{7}$ + {3$\frac{3}{7}$ ÷ (2$\frac{4}{7}$ – $\frac{1}{7}$)}

28. 18 + [3 – {1 + (4 × $\frac{3}{16}$)}]

29. 95 – [4$\frac{1}{2}$ + {4 (7 + 5 – 3$\frac{1}{2}$)}]

30. 40 + [3 {2 (20 ÷ 3$\frac{1}{3}$)}]

31. $\frac{1}{3}$ + [3$\frac{1}{3}$ + {4 (18 – 9$\frac{1}{3}$)}]

32. 32$\frac{1}{2}$ + [4 {2 (11 × 9$\frac{1}{3}$)}]

33. 35 + [3$\frac{1}{4}$ of {6 – 3 (9 – $\overline{6 + 3}$)}]

34. 19 + [6 {3 + ($\frac{5}{16}$ of 64)}]

35. 18 + [5$\frac{1}{5}$ of {7 – 2(8 – $\overline{4 + 2}$)}]

36. 24 + [6 {4 + ($\frac{3}{8}$ × 56)}]

37. $\frac{4}{15}$ + {3 ($\frac{4}{5}$ of 25)} ÷ $\frac{20}{23}$

38. 1$\frac{1}{2}$ {3$\frac{9}{10}$ – (4$\frac{1}{2}$ + – $\overline{5\frac{1}{5} ÷ 2\frac{3}{5}}$)}

39. 3$\frac{3}{8}$ + {4 ($\frac{1}{8}$ of 32)} ÷ $\frac{1}{3}$

40. $\frac{3}{7}$ + {4 ($\frac{2}{5}$ × 25)} ÷ $\frac{1}{10}$

41. 1$\frac{1}{5}$ × (2$\frac{1}{12}$ ÷ $\frac{5}{12}$) + 3 ($\frac{1}{12}$ – $\frac{1}{15}$)

42. (3$\frac{2}{3}$ ÷ 1$\frac{2}{3}$) + ($\frac{1}{3}$ × $\frac{1}{6}$) + ($\overline{1\frac{1}{3} – \frac{1}{3}}$)

Students can check the answers of the worksheet on simplification given below to make sure that the answers are correct.

$Worksheet on Simplification$

Worksheet on Simplification Answer:

A. 1. 0

2. -18

3. 24

4. 35

5. 21

6. 26

7. 46

8. 2370

9. 10

10. 24

11. 62

12. 1

B. 1. 9(2 + 5)

2. 12 ÷ (1 + 3)

3. 20 ÷ (7 – 2)

4. 2 x 3 – 8

5. 40 ÷ {1 + (9 + 10)}

6. 2 x {(19 – 6) – 1}

C. 1. 6($\frac{9}{16}$

2. 1($\frac{77}{360}$

3. 124

4. 22050

5. 24

6. 5$\frac{1}{12}$

7. 41$\frac{1}{2}$

8. 296$\frac{11}{27}$

9. 20

10. 44

11. 408

12. 36

13. 14$\frac{1}{4}$

14. 78$\frac{1}{3}$

15. 19$\frac{4}{5}$

16. 6$\frac{2}{15}$

17. 7$\frac{1}{72}$

18. 30$\frac{7}{10}$

19. 8$\frac{11}{16}$

20. $\frac{7}{28}$

21. 1$\frac{1}{20}$

22. 2$\frac{8}{9}$

23. 46$\frac{179}{198}$

24. 2$\frac{2}{9}$

25. 5$\frac{1}{2}$

26. 30$\frac{1}{4}$

27. 5$\frac{66}{119}$

28. 19$\frac{1}{4}$

29. 56$\frac{1}{2}$

30. 76

31. 38$\frac{1}{3}$

32. 853$\frac{5}{6}$

33. 54$\frac{1}{2}$

34. 157

35. 33$\frac{3}{5}$

36. 174

37. 69$\frac{4}{15}$

38. 2$\frac{1}{10}$

39. 51$\frac{3}{8}$

40. 400$\frac{3}{7}$

41. 6$\frac{1}{20}$

42. 3$\frac{23}{90}$

If students have any queries regarding the questions given in the worksheet on simplification, please fill-up the bellow comment box so that we can help you.

However, suggestions for further improvement, from all quarters would be greatly appreciated.

Answer:

BODMAS helps us solve mathematical expressions in the correct order:
B – Brackets, O – Orders, D – Division, M – Multiplication, A – Addition, S – Subtraction.

This rule is very useful in daily life when we calculate money, shopping bills, discounts, and measurements.

● Numbers – Integers

Integers

Multiplication of Integers

Properties of Multiplication of Integers

Examples on Multiplication of Integers

Division of Integers

Absolute Value of an Integer

Comparison of Integers

Properties of Division of Integers

Examples on Division of Integers

Fundamental Operation