Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In real life situations, we come across many instances where representing the opposites are of great need. If we measure the heights of buildings, mountains, etc., above sea-level, we have to measure depth below sea-level. When temperatures are measured above 0°C, the temperatures go down below 0°C in certain places. To represent all these distinctly, we need some other measures along with whole numbers, i.e., as the opposites of them. Hence, negative numbers are created. Thus, we have -1 as the opposite of +1, -2 as the opposite of +2, -3 as the opposite of +3 and so on.
Note: Zero is considered neither negative nor positive.
Connection of Negative Numbers in Daily Life:
The negative numbers show the oppositeness of the positive numbers. Hence, the positive and negative quantities are used in opposite sense.
For example:
✅ Temperature above 0°C is taken as positive, while that below 0°C is taken as negative.
✅ Profit is expressed as positive, while loss is expressed as negative.
✅ Depositing money in a bank is considered positive, while withdrawal of money is taken as negative.
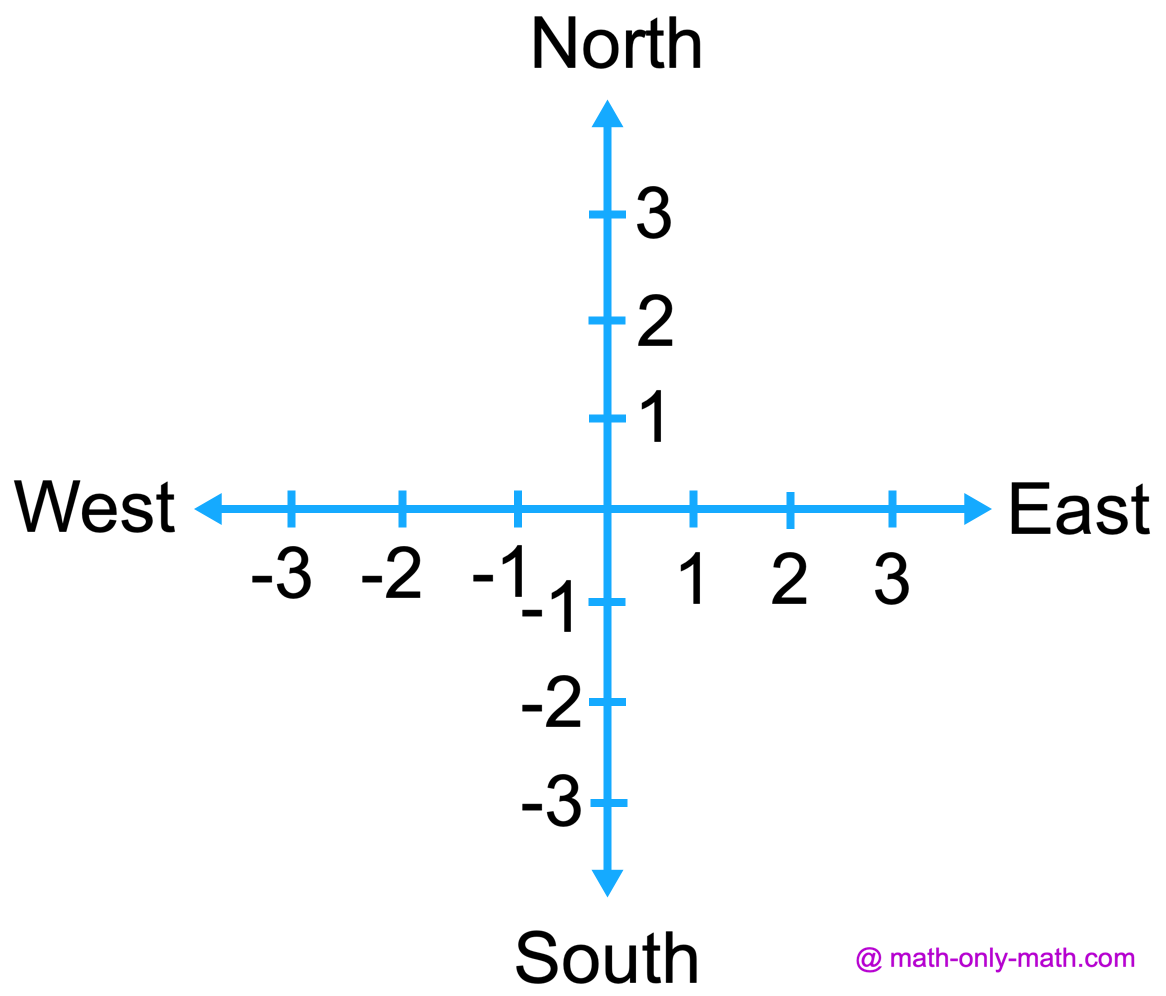
✅ Walking towards north is considered as positive, while towards south as negative. Similarly, walking towards east is considered as positive and walking towards west is negative.
✅ Height above sea-level is taken as positive, while that below sea-level is taken as negative.
Representation Of Negative Numbers On Number Line:
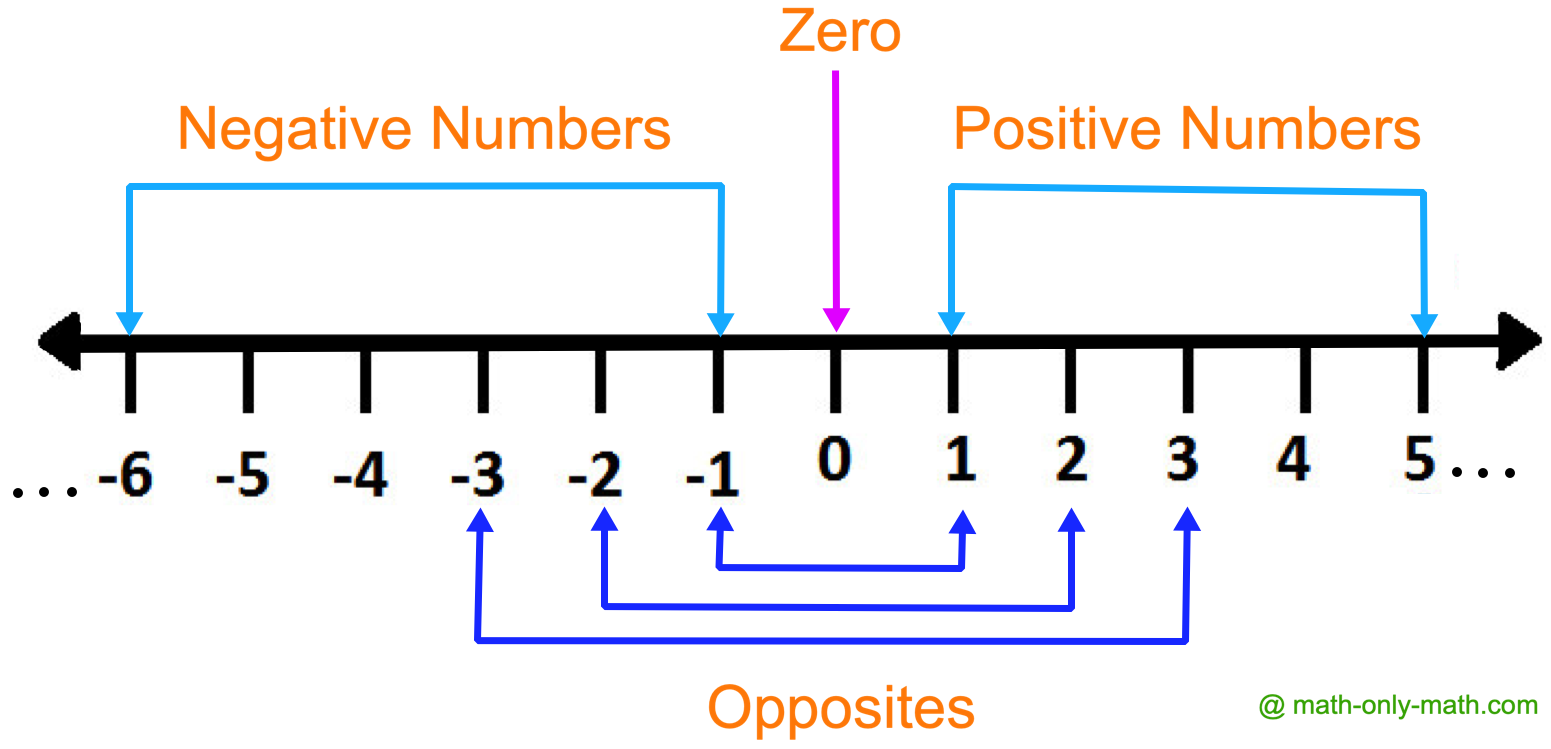
The numbers less than 0 can be represented as the negative numbers. So, -1, -2, -3, -4, -5, … are the negative numbers, which are shown by affixing minus sign (-) with the natural numbers.
These negative numbers can be represented on the number line as shown below. On moving 1 step towards left starting from 0 we get -1, 2 steps towards left starting from 0 we get -2, 3 steps towards left starting from 0 we get -3, so on.
Thus, all other negative numbers can be represented on the number line to the left of 0.
Ordering of Negative Numbers:
Just like whole numbers, a negative number on the number line is greater than the number to its left or less than the number to its right.
For example, -1 > -2 or -2
Hence, we have the following ordering of negative numbers:
-1 > -2 > -3 > -4 > -5 … or … -5
Oppositeness of Positive and Negative Numbers on Number Line:
Look at the number line below:
On the number line, 0 is considered the starting point. To the right of 0, the points as 1, 2, 3, 4, 5, 6, … are labelled. To the left of 0, lies -1. It is at the same distance from 0 as 0 from 1. To the left of -1, lies -2, -3, -4, and so on. From the number line, it is clear that the numbers -1, -2, -3, .. are equidistant from 0 as the numbers 1, 2, 3, … but in opposite direction. Thus, the numbers to the left of 0, i.e., -1, -2, -3, … are opposites of the numbers to the right of 0, i.e., 1, 2, 3, … and vice-versa.
Note: Zero is neither positive nor negative.
From Negative Numbers on Number Line to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.